IEEE浮点表示 （原发布 csdn 2018-10-14 10:29:33）

目录

• 观察IEEE浮点表示
  • 工作中遇到过整型转浮点型(union那种转换)，碰到就看下书，过后就遗忘了。等过段时间又出现此现象，又重新拿起书本，这次记录了过程。然而一直等到今天才写出来，以防以后还用到，如果能帮助到你就更好了。
    • 测试代码
    • 思路
    • 结果
    • 参考资料

@(IEEE浮点表示)

观察IEEE浮点表示

工作中遇到过整型转浮点型(union那种转换)，碰到就看下书，过后就遗忘了。等过段时间又出现此现象，又重新拿起书本，这次记录了过程。然而一直等到今天才写出来，以防以后还用到，如果能帮助到你就更好了。

测试代码

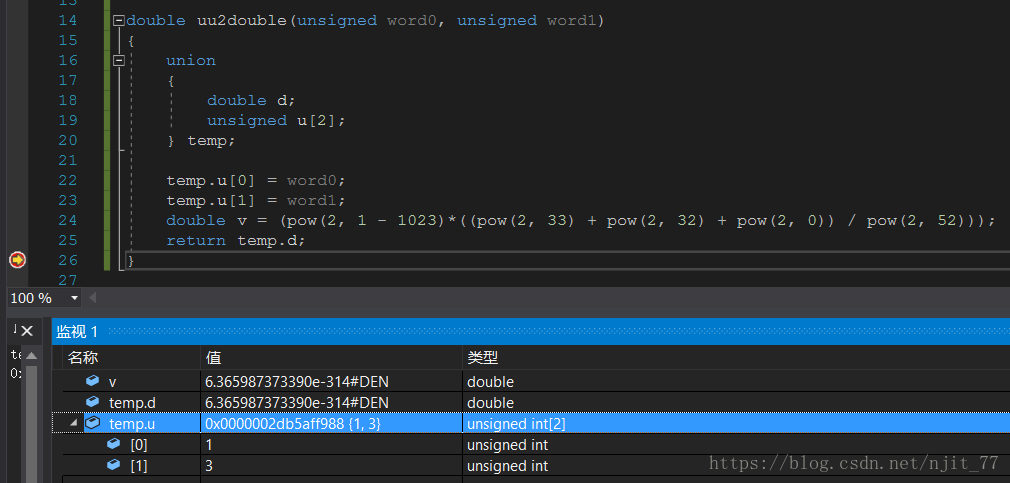
double uu2double(unsigned word0, unsigned word1)
{
    union
    {
        double d;
        unsigned u[2];
    } temp;

    temp.u[0] = word0;
    temp.u[1] = word1;
    return temp.d;
}

思路

1,3(小端模式)

//unsigned 4字节 
//  u[1]                                       u[0]
00 00 00 03                                 00 00 00 01

//double   8字节
//d
0000 0000 0000 0000 0000 0000 0000 0011 0000 0000 0000 0000 0000 0000 0000 0001

//IEEE 浮点表示
/*
  V = (-1)^s * M * 2^E
  符号（sign） 负数(s=1)、正数(s=0)
  规格化的值(阶码域exp不全是0，也不全是1):   E = e-Bias(2^(k-1)-1  单精度127，双精度1023)，M = 1+f
  非规格化的值(阶码域exp全是0):             E = 1-Bias(2^(k-1)-1  单精度127，双精度1023)，M = f
*/
//符号s     阶码exp                         尾数f
    0     00000000000   0000 0000 0000 0000 0011 0000 0000 0000 0000 0000 0000 0000 0001
    
    非规格化 V = {2^(1-1023)*[(2^32+2^31+2^0)/(2^52)]} = 6.365987373390e-314#DEN

结果

参考资料

深入理解计算机系统(中文，原书第三版)

原文链接:https://www.cnblogs.com/njit-77/p/11469092.html
如有疑问请与原作者联系

标签：

版权申明：本站文章部分自网络，如有侵权，请联系：west999com@outlook.com
特别注意：本站所有转载文章言论不代表本站观点，本站所提供的摄影照片，插画，设计作品，如需使用，请与原作者联系，版权归原作者所有