首页 > > 程序设计 > C/C++ >

洛谷P1731 [NOI1999]生日蛋糕(爆搜)

2018-07-06 01:20:23来源：博客园阅读 ()

题目背景

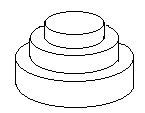
7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层

生日蛋糕，每层都是一个圆柱体。

设从下往上数第i(1<=i<=M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i<M时，要求 $R_i>R_{i+1}Ri?>Ri+1? 且 H_i>H_{i+1}Hi?>Hi+1? 。$

由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。

令Q= Sπ

请编程对给出的N和M，找出蛋糕的制作方案（适当的Ri和Hi的值），使S最小。

（除Q外，以上所有数据皆为正整数）

题目描述

输入输出格式

输入格式：

有两行，第一行为N（N<=20000），表示待制作的蛋糕的体积为Nπ；第二行为M(M<=15)，表示蛋糕的层数为M。

输出格式：

仅一行，是一个正整数S（若无解则S=0）。

输入输出样例

输入样例#1：复制

100
2

输出样例#1：复制

emmmm不会做。。。

直到看了标签是“搜索”。。。

那就开心的搜吧。。

可以推出式子

$$N = \sum_{i = 1}^M R_i * R_i * H_i$$

$$S = R_1^2 + 2 * \sum_{i = 1}^M R_i H_i$$

时间复杂度：$O(玄学)$

#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
#include<map>
#include<cmath>
#define LL long long 
using namespace std;
const int MAXN = 1e6 + 10, INF = 1e9 + 10;
inline int read() {
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int N, M;
int H[16], R[16];
int ans = INF;
void dfs(int now, int sum, int nowans) {
    if(sum > N || (nowans + R[1] * R[1]) > ans) return ;
    if(now == M + 1) {
        if(sum == N) 
            ans = min(ans, nowans + R[1] * R[1]); 
        return ;
    }
    if(sum + R[now - 1] * R[now - 1] * H[now - 1] * (M - now + 1) < N) return ;
    //如果后面都用最大的体积仍然不能达到要求
    if(nowans + (M - now + 1) + R[1] * R[1] > ans) return ; 
    //加上最小的仍然大于答案 
    for(int i = M - now + 1; i < H[now - 1]; i++) {
        for(int j = M - now + 1; j < R[now - 1]; j++) {
            H[now] = i; R[now] = j;
            dfs(now + 1, sum + R[now] * R[now] * H[now], nowans + 2 * R[now] * H[now]);
            H[now] = 0; R[now] = 0;
        }
    }
}
main() {
#ifdef WIN32
    //freopen("a.in", "r", stdin);
#endif 
    
    N = read(); M = read();
    H[0] = sqrt(N); R[0] = sqrt(N);
    dfs(1, 0, 0);
    printf("%d", ans == INF ? 0 : ans);
    return 0;
}