首页 > > 程序设计 > C/C++ >

【luogu 3382】【模板】三分法

2018-06-17 21:48:28来源：未知阅读 ()

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

输入样例#1：

3 -0.9981 0.5
1 -3 -3 1

输出样例#1：

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

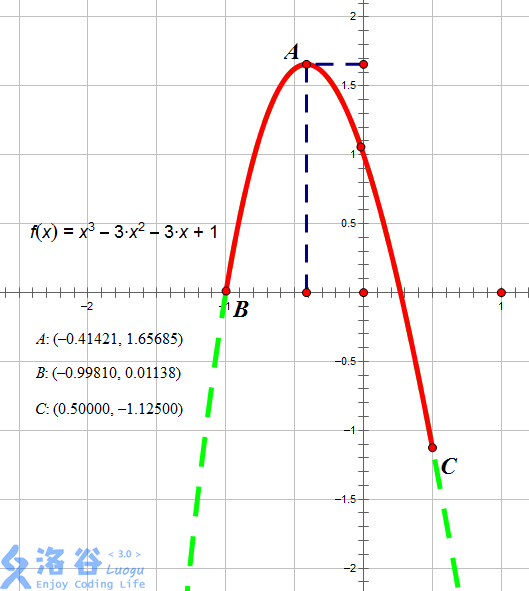
如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

题解：

裸三分。

在[L,R]中，

取a=(R-L)/3+L,b=(R-L)/3*2+L。

如果f(a)>f(b)

则答案在[L,b]里（如果在[b, R]里，则[a, b]段递增），

如果f(a)<f(b)

则答案在[a,R]里（如果在[L, a]里，则[a, b]段递减），

递归或循环即可。

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<algorithm>
 5 #include<cmath>
 6 using namespace std;
 7 double l,r,xs[23];int n;
 8 double f(double x){
 9     double ans=0;
10     for(int i=1;i<=n;i++){
11         double tmp=xs[i];
12         for(int j=1;j<=n-i+1;j++) tmp*=x;
13         ans+=tmp; 
14     }
15     return ans+xs[n+1];
16 }
17 int main(){
18     scanf("%d",&n);
19     scanf("%lf%lf",&l,&r);
20     for(int i=1;i<=n+1;i++) scanf("%lf",&xs[i]);
21     double lx=l,rx=r;
22     while(abs(lx-rx)>0.000001){
23         double x1=(rx-lx)/3+lx,x2=(rx-lx)/3*2+lx;
24         if(f(x1)>f(x2)) rx=x2;
25         else lx=x1;
26     }
27     printf("%.5f\n",lx);
28     return 0;
29 }