首页 > > 程序设计 > C/C++ >

Luogu 2296 寻找道路

2018-06-17 21:36:23来源：未知阅读 ()

https://www.luogu.org/problemnew/show/2296

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目?述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：复制

输出样例#1：复制

-1

输入样例#2：复制

输出样例#2：复制

说明

解释1：

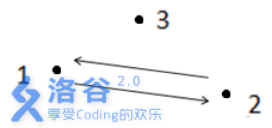
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目?述的路径不存在，故输出- 1 。

解释2：

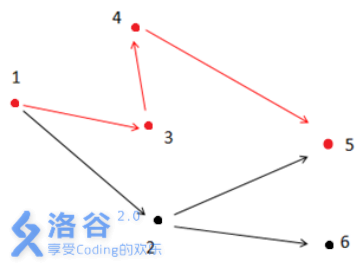
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

这道题做了一个下午，思路不是很清晰。后来看了题解才有思路。代码也是很好写的。

我们发现“不能通过的点”特征是：1.无出度 2.不是终点（仔细想想）

然后再把与“不能通过的点”直接标记，再标记与之相邻的点（反向存图就可以找与之相邻的点了）

再用spfa在未标记的点中寻找最短路就ok了

其他细节见代码

#include<iostream>
#include<queue>
using namespace std;
int to[10001][10001],inde[10005],outde[10005],to2[10001][10001],flag[10005],outde2[10005];
//to 用来存图 inde 入度 outde出度 to2反向图 flag 标记 outde2反向出度
int dis[10001],vis[10001];//spfa 操作
int top=1,maxn = 200070;
int n,m;
int b,e;
void spfa(int s)
  {
      queue<int> q;
      q.push(s);
      vis[s] = 1;
      dis[s] = 0;
      while(!q.empty())
        {
        int now,next; now = q.front(); q.pop(); vis[now] = 0;
        for(int i = 1;i <= outde[now];i++)
         {
                  next = to[now][i];
            if(!flag[next])
              {
                  if(dis[next] > dis[now]+1)
                   {
                       dis[next] = dis[now] + 1;
                       if(!vis[next])
                         {
                             q.push(next);
                             vis[next] = 1;
                         }
                   } 
              } 
        }
        }
  }
void first()//预处理
  {
      for(int i = 1;i <= n;i++)
        {
            dis[i] = maxn; //在这里初始化dis[i]
            if (outde[i] == 0 && i != e)
                 {
               flag[i] = 1;
               for(int j = 1;j <= outde2[i];j++)//反向找与之直接相邻的点
               flag[to2[i][j]] = 1;
                 } 
        }
  }
int main()
  {
      cin>>n>>m;
      for(int i = 1;i <= m;i++)
       {
           int x,y;
           cin>>x>>y;
           outde[x] ++;
           outde2[y] ++;
           to[x][outde[x]] = y;
           to2[y][outde2[y]] = x;
           inde[y] ++;
       }
       cin>>b>>e;
       first();
       spfa(b);
       if(dis[e] != maxn) cout<<dis[e];
        else cout<<-1;
        return 0;
  }