洛谷P3382 【模板】三分法(三分)

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

3 -0.9981 0.5
1 -3 -3 1

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

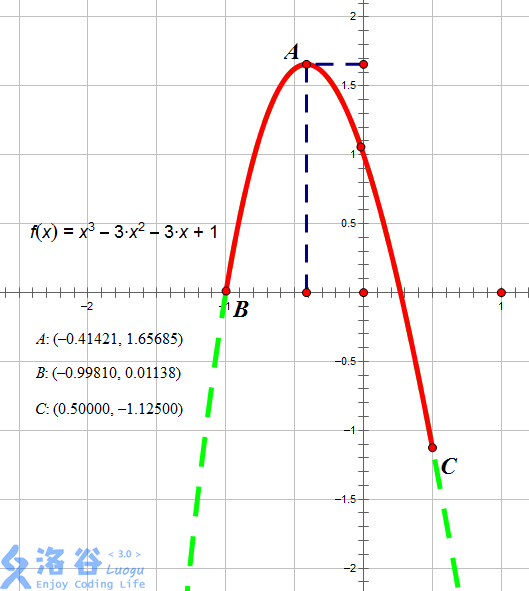
如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

（Tip.l&r的范围并不是非常大ww不会超过一位数）

不会三分好吃亏啊。

三分其实很简单

对于一个二次函数

在$[L,R]$内取最值，选取两个点$$x = (2 * l + r) / 3, y = (l + 2 * r) / 3$$

若$f(x)>f(y)$，那么$[y,R]$这一段可以舍弃(一定不会成为最优解)，否则$[l,x]$这一段舍弃

#include<cstdio>
#define abs(x) x < 0 ? -x : x
int N;
double a[13], l, r;
double f(double x) {
    double ans = 0;
    for(int i = N; i >= 0; i--) ans = ans * x + a[i];    
    return ans;
}
main() {
    scanf("%d %lf %lf", &N, &l, &r);
    for(int i = N; i >= 0; i--) scanf("%lf", &a[i]);
    while(abs(r - l) > 1e-12) {
        double x = (2 * l + r) / 3, y = (l + 2 * r) / 3;
        f(x) > f(y) ? r = y : l = x;
    }
    printf("%.5lf", l);
}

标签：

版权申明：本站文章部分自网络，如有侵权，请联系：west999com@outlook.com
特别注意：本站所有转载文章言论不代表本站观点，本站所提供的摄影照片，插画，设计作品，如需使用，请与原作者联系，版权归原作者所有